When developing mathematical models of reality, at the forefront of your mind must be the question you are aiming to answer. The model must be sufficiently complex to respond to this question. As an example we will look at the question of climate change attribution, that is:
- Did human activities cause the global temperature increase over the passed 100 years?
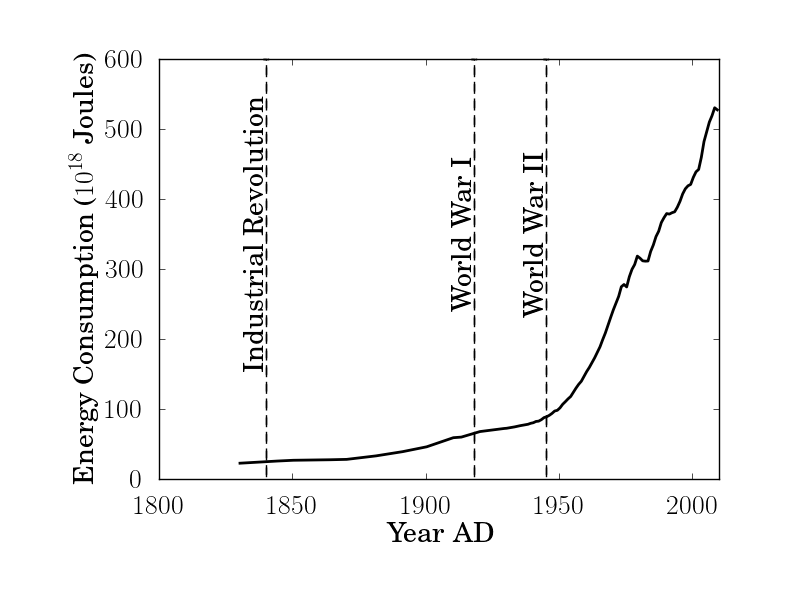
As I discussed in the previous post over the passed 100 years the human population has increased from 2 billion to 7 billion people, and our total energy consumption has increased over 10 fold. The burning of fossil fuels to meet this energy consumption need rapidly increased the carbon dioxide concentration in the atmosphere to a level higher than anything observed over the passed 700,000 years. More carbon dioxide in the atmosphere enhances the greenhouse effect, which traps in more heat from the sun, and increases the temperature of the planet. The question remains, however, is the observed increase in temperature over the passed 100 years due to man made carbon dioxide emissions, or would the Earth have heated up anyway? We do not have another Earth without man made carbon dioxide emissions to directly compare to, so to help us answer this question we rely on numerical simulations of a virtual Earth.
The diagram below outlines the general steps in developing a mathematical representation of any system. It is a simplified version of that presented in reference [1] below. One starts with "reality" in all its complexity and splendour. In order to answer the desired question it is not necessary to retain all of this complexity and we can simply our view of the world. For example we need to include the effect of heating from the sun, and the greenhouse effect as a result of carbon dioxide emissions from both natural processes and human activities. On the other hand we do not need to model the combustion process generating the emissions from each individual manufacturing plant, house and car. It is sufficient to use the measured carbon dioxide concentration in the atmosphere as an input. This simplified view is what is called the "conceptual model".
The next step is to represent our idealised view of the world with mathematics. This "mathematical model" is a set of equations that governs how the winds, rain and temperature of the Earth changes in time and space. These are very complicated equations and do not have a simple analytical solution that one can write down on paper. We, therefore, need to develop a "numerical model", which breaks the Earth down into a series of discrete positions in space and time. For example we can break the Earth down into a series of horizontal boxes of size 100km, and in time by solving the equations once every day or so. The greater the resolution, that is the smaller the boxes and shorter the time step, the more accurate the "numerical model". The "numerical model" is essentially software that solves the discrete equations on a computer. In this particular application, the "numerical model" is referred to as a general circulation model, which was specifically discussed in my second post. The following "numerical solution" is the final data generated by the "numerical model", which we can later analyse and data mine.
At each step we make assumptions in order to represent "reality" by a "numerical solution". The potential error associated with each of these assumptions must also be assessed to determine if one can respond to the original question given the amount of uncertainty. One way of doing this is to test the sensitivity of the assumptions to the final result. An example of quantifying this uncertainty is presented below for the climate attribution problem. The following graphs are generated by the Intergovernmental Panel on Climate Change (IPCC) effort published in reference [2] listed at the end of this post.
The black line in the figure below represents the observed increase in temperature of the planet from 1900. Each thin orange line represents the temperature resulting from one of 58 "numerical solutions" with different resolutions in space and time, generated by 14 different "numerical models" solving different specific equations using different numerical techniques. The thick red line is the average temperature of all of the cases. These simulations include the carbon dioxide originating from both natural processes and also from human activities (i.e. burning fossil fuels). As you can see there is quite a bit of variability between each of the 58 simulations, but on average they follow the observed changes quite well. Interestingly, the vertical grey lines identify major volcanic eruptions, which coincide with a temperature decrease in both the observations and the simulations. This is because the volcanoes send up so much dust, dirt and other particles into the atmosphere that they essentially block out the Sun for extended periods of time, which temporarily reduces the temperature.
In contrast, the figure below illustrates the temperature generated from simulations that do not include carbon dioxide from human activities. Each light blue lines represents one of 19 "numerical solutions" from 5 different "numerical models", with the thick blue line the average. As you can see the agreement with the observations is not very good, with the general trend not agreeing with the observations. Whilst there is again a significant amount of variability between each of the different cases, not any one of the simulations are able to reproduce the observed warming. So after accounting for the uncertainty the only way to reproduce the observed warming over the passed century is to include man made carbon dioxide emissions. In other words, the Earth would not have heated up without human involvement. This is an example of the numerical solutions having sufficiently high fidelity and sufficiently low uncertainty to answer the original question.
Globally averaged temperature is quite a robust signal. However, there is more model variability / uncertainty when asking the question if a particular place will be hotter, colder, wetter or drier. For example under a warming world there will be more evaporation, which means more water vapour in the atmosphere, which also means more rain. However, it is not clear if a particular place will receive more or less rain, as the patterns of rainfall are also likely to change. So it may well be raining more around the world on average, but it might be raining more over the ocean and less is certain places over land. This is precisely what is happening in the southern hemisphere. The weather patterns are changing such that the rain that was previously falling over the south-west of Australia has shifted further south, and is it now raining more over the ocean - see reference [3] below. It is very difficult to predict how this will change in the future. Each of the global circulation models may suggest similar increases in total global rainfall, but the rainfall patterns are very different. This means less agreement and more uncertainty on the predicted rainfall for a particular place in the world in the future.
References:
[1] B. H. Thacker, S. W. Doebling, F. M. Hemez, M. C. Anderson, J. E. Pepin, E. A. Rodriguez, 2004, "Concepts of Model Verification and Validation", Los Alamos Laboratory Technical Report.
[2] Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, 2007, Solomon, S., D. Qin, M. Manning, Z. Chen, M. Marquis, K.B. Averyt, M. Tignor and H.L. Miller (eds.) Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA.
[3] J. S. Frederiksen and C. S. Frederiksen, “Decadal changes in Southern Hemisphere winter cyclogenesis,” in CSIRO Marine and Atmospheric Research, p. 29, Aspendale, Victoria, Australia, 2005